Statistical Process Control

There are three types of control charts used determine if data is out of control, $x$-bar charts, $r$-charts and $s$-charts. An $x$-bar chart is often paired with either an $r$-chart or an $s$-chart to give a complete picture of the same set of data.

Pairing $X$-Bar with $R$-Charts

$X$-Bar (average) charts and $R$ (range) -charts are often paired together. The $X$-Bar chart displays the centerline, which is calculated using the grand average, and the upper and lower control limits, which are calculated using the average range. Future experimental subsets are plotted compared to these values. This demonstrates the centering of the subset values. The $R$-chart plots the average range and the limits of the range. Again, the future experimental subsets are plotted relative to these values. The $R$-chart displays the dispersion of the subsets. $X$-Bar/$R$-Chart plot a subgroup average. Note that they should only be used when subgroups really make sense. For example, in a Gage R&R study, when operators are testing in duplicates or more, subgrouping really represents the same group.

Pairing $X$-Bar with $S$-Charts

Alternatively, $X$-Bar charts can be paired with $S$-charts (standard deviation). This is typically done when the size of the subsets are large. For larger subsets, the range is a poor statistic to estimate the distributions of the subsets, and instead, standard deviation is used. In this case, the $X$-Bar chart will display control limits that are calculated using the average standard deviation. The $S$-Charts are similar to the $R$-charts; however, instead of the range, they track the standard deviation of multiple subsets.

Smoothing Data with a Moving Average

If it is desired to have smooth data, the moving average method is one option. This method involves taking the average of a number of points, and using that average for the middle data point. From this point on, the data is treated the same as any normal group of $k$ subsets. Though this method will produce a smoother curve, it has a lag in detecting points, which may be problematic if the points are out of the acceptable range. This time lag would keep the control system from reacting to the problem until after the average is found. For this reason, moving average charts are appropriate mainly for slower processes that can handle the lag.

Reading Control Charts

Control charts can determine whether a process is behaving in an "unusual" way.

Note: The upper and lower control limits are calculated using the grand average and either the average range and average sigma. Example calculations are shown in the Creating Control Charts Section.

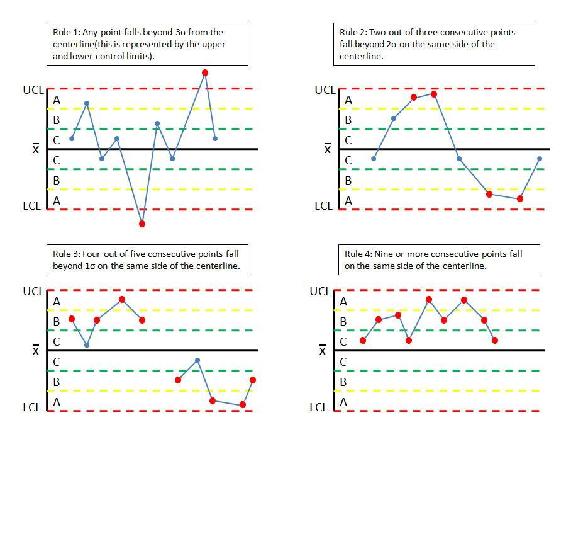
The quality of the individual points of a subset is determined unstable if any of the following occurs:

• Rule 1: Any point falls beyond $3\sigma$ from the centerline(this is represented by the upper and lower control limts).
• Rule 2: Two out of three consecutive points fall beyond $2\sigma$ on the same side of the centerline.
• Rule 3: Four out of five consecutive points fall beyond $1\sigma$ on the same side of the centerline.
• Rule 4: Nine or more consecutive points fall on the same side of the centerline.

The quality of a subset is determined unstable according to the following rules:

1. Any subset value is more than three standard deviations from the centerline.

2. Two consecutive subset values are more than two standard deviations from the centerline and are on the same side of the centerline.

3. Three consecutive subset values are more than one standard deviation from the centerline and are on the same side of the centerline.

Creating Control Charts

To establish upper and lower control limits on control charts, there are a number of methods. We will discuss the method for the number of components in a subset, $n$, less than $15$. For methods involving $n > 15$ and other techniques, see Process Control and Optimization, Liptak, 2.34. Here, the table of constants for computing limits, and the limit equations are presented below.

Please note that Table A below does NOT contain data for a sample problem. Any time you make a control chart, you refer to this table. The values in the table are used in the equations for the upper control limit (UCL), lower control limit (LCL), etc. This will be explained in the examples below. If you are interested in how these constants were derived, there is a more detailed explanation in Control Chart Constants.

Table A: Table of Constants

To determine the value for $n$, the number of subgroups

In order to determine the upper (UCL) and lower (LCL) limits for the $x$-bar charts, you need to know how many subgroups ($n$) there are in your data. Once you know the value of $n$, you can obtain the correct constants (A2, A3, etc.) to complete your control chart. This can be confusing when you first attend to create a $x$-bar control chart. The value of $n$ is the number of subgroups within each data point. For example, if you are taking temperature measurements every min and there are three temperature readings per minute, then the value of $n$ would be. And if this same experiment was taking four temperature readings per minute, then the value of $n$ would be $4$. Here are some examples with different tables of data to help you further in determining $n$:

Example 1: $n= 4$ since there are four readings of kg.

Example 2: $n= 4$ since there are four readings of pH.

Example 3: $n= 3$ since there are three readings of temperature.

After creating multiple control charts, determining the value of n will become quite easy.

Calculating UCL and LCL

For the $X$-Bar chart the following equations can be used to establish limits, where $X_{G A}$ is the grand average, $R_{A}$$ is the average range, and $S_{A}$ is the average standard deviation.

Calculating Grand Average, Average Range and Average Standard Deviation

To calculate the grand average, first find the average of the n readings at each time point. The grand average is the average of the averages at each time point.

To calculate the grand range, first determine the range of the n readings at each time point. The grand range is the average of the ranges at each time point.

To calculate the average standard deviation, first determine the standard deviation of the $\mathbf{n}$ readings at each time point. The average standard deviation is the average of the standard deviations at each time point.

Note: You will need to calculate either the grand range or the average standard deviation, not both.

For $X$-bar charts, the UCL and LCL may be determined as follows:

$\begin{aligned}&\text { Upper Control Limit }(\mathrm{UCL})=X_{G A}+A_{2} R_{A} \\&\text { Lower Control Limit }(\mathrm{LCL})=X_{G A}-A_{2} R_{A}\end{aligned}$

Alternatively, $S_{A}$ can be used as well to calculate UCL and LCL:

$\text { Upper Control Limit (UCL) }=X_{G A}+A_{3} S_{A}$

$\text {Lower Control Limit (LCL) }=X_{G A}-A_{3} S_{A}$

The centerline is simply $X_{G A}$.

For $R$-charts, the $U C L$ and $L C L$ may be determined as follows:

$\begin{aligned}\mathrm{UCL} &=D_{4} R_{A} \\\mathrm{LCL} &=D_{3} R_{A}\end{aligned}$

The centerline is the value $R_{A}$.

For $S$-charts, the $U C L$ and $L C L$ may be determined as follows:

$\begin{aligned}&\mathrm{UCL}=B_{4} S_{A} \\&\mathrm{LCL}=B_{3} S_{A}\end{aligned}$

The centerline is $S_A$.

The following flow chart demonstrates the general method for constructing an $X$-bar chart, $R$-chart, or $S$-chart:

Calculating Region Boundaries

To determine if your system is out of control, you will need to section your data into regions A, B, and C, below and above the grand average. These regions are shown in Figure III. To calculate the boundaries between these regions, you must first calculate the UCL and LCL. The boundaries are evenly spaced between the UCL and LCL. One way to calculate the boundaries is shown below.

Boundary between A and B above $X_{G A}=X_{G A}+\left(U C L-X_{G A}\right) * 2 / 3$

Boundary Between B and C above $X_{G A}=X_{G A}+\left(U C L-X_{G A}\right) * 1 / 3$

Boundary Between A and B below $X_{G A}=\angle C L+\left(X_{G A}-L C L\right) * 2 / 3$

Boundary Between B and C below $X_{G A}=L C L+\left(X_{G A}-L C L\right) * 2 / 3$