Print this chapterPrint this chapter

Forward and Futures Contracts

Finance Theory

Valuation of Forwards and Futures

What Determines Forward and Futures Prices?

  • Forward/futures prices ultimately linked to future spot prices
  • Notation:

    Contract Spot at t
    		 Forward Futures
    Price S_t F_{t,T} H_{t,T}

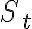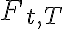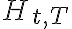  • Ignore differences between forward and futures price for now
    F_{t,T} \approx. H_{t, T}
  • Two ways to buy the underlying asset for date-T delivery
    1. Buy a forward or futures contract with maturity date T
    2. Buy the underlying asset and store it until T
Date Forward Contract
Outright Asset Purchase
0
  • Pay $0 for contract with forward price $F0,T
  • Borrow $S0
  • Pay $S0 for Asset
T
  • Pay $F0,T
  • Own asset
  • Pay back $S0(1+r)T
  • ƒPay cumulative storage costs (if any)
  • ƒDeduce cumulative" convenience yield" (if any)
  • ƒOwn asset
Total Cost at T
  $F0,T $S0(1+r)T   +  net storage costs

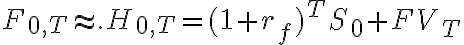
F_{0,T} \approx. H_{0, T} = (1+r_f)^T S_0 + FV_T (net storage costs)

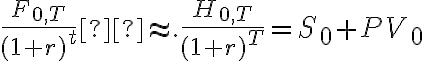
\dfrac{F_{0,T}}{(1+r)^t}  \approx. \dfrac{H_{0, T}}{(1+r)^T} = S_0 + PV_0 (net storage costs)


Date Forward Contract
Outright Asset Purchase
t
  • Pay $0 for contract with forward price $Ft,T
  • Borrow $St
  • Pay $St for Asset
T
  • Pay $Ft,T
  • Own asset
  • Pay back $St(1+r)T-t
  • ƒPay cumulative storage costs (if any)
  • ƒDeduce cumulative" convenience yield" (if any)
  • ƒOwn asset
Total Cost at T
  $Ft,T $S0(1+r)T-t   +  net storage costs

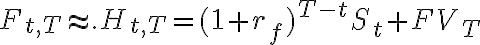
F_{t,T} \approx. H_{t, T} = (1+r_f)^{T-t} S_t + FV_T (net storage costs)

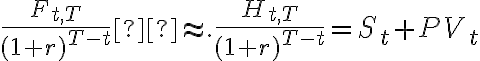
\dfrac{F_{t,T}}{(1+r)^{T-t}}  \approx. \dfrac{H_{t, T}}{(1+r)^{T-t}} = S_t + PV_t (net storage costs)

What Determines Forward/Futures Prices?

  • Difference between the two methods:
    – Costs (storage for commodities, not financials)
    – Benefits (convenience for commodities, dividends for financials)
  • By no arbitrage (Principal P1), these two methods must cost the same

Gold

  • Easy to store (negligible costs of storage)
  • No dividends or benefits
  • Two ways to buy gold for T
    – Buy now for S tand hold until T
    – Buy forward at t, pay Ft,T at T and take delivery at T
  • No-arbitrage requires that
F_{t,T} \approx. H_{t, T} = (1+r_f)^{(T-t)} S_t


Gasoline
  • Costly to store (let c be percentage cost per period)
  • Convenience yield does exist (let ybe percentage yield per period)
  • Not for long-term investment (like gold), but for future use
  • Two ways to buy gasoline for T
    – Buy now for S tand hold until T
    – Buy forward at t, pay Ft,T at T and take delivery at T
  • No-arbitrage requires that
F_{t,T} \approx. H_{t, T} = (1+r_f + c - y)^{(T-t)} S_t

Financials

  • Let underlying be a financial asset
    – No cost to store (the underlying asset)
    – Dividend or interest on the underlying
  • Example: Stock index futures
    – Underlying are bundles of stocks, e.g., S&P, Nikkei, etc.
    – Futures settled in cash (no delivery)
    – Let the annualized dividend yield be d; then

    F_{t,T} \approx. H_{t, T} = (1+r_f -d)^{(T-t)} S_t

Example:

  • Gold quotes on 2001.08.02 are
  • Spot price (London fixing) $267.00/oz
  • October futures (CMX) $269.00/oz
  • What is the implied interest rate?
F=S_0(1+r_f)^{2/12}
r_f= ( F/S_0)^6 −1 = 4.58%

Example:

  • Gasoline quotes on 2001.08.02:
  • Spot price is 0.7760
  • Feb 02 futures price is 0.7330
  • 6-month interest rate is 3.40%
  • What is the annualized net convenience yield (net of storage costs)?
0.7330=(0.7760)(1+0.0340−y)^{6/12}

y= 1 .0340− (\dfrac{0.7330}{0.7760})^2 = 14.18%

Example:

  • The S&P 500 closed at 1,220.75 on 2001.08.02
  • The S&P futures maturing in December closed at 1,233.50
  • Suppose the T-bill rate is 3.50%
  • What is the implied annual dividend yield?
d  = [1+r_f - (f/S_0)^{12/4}]
= [1 + 0.0350 - (1233.50/1220.75)^3] = 0.33%