Statistical Inference about Slope
This section further details two types of inferences on the slope parameter, considering both confidence intervals and hypothesis testing.
Statistical Inferences About β1
Learning Objectives
- To learn how to construct a confidence interval for
, the slope of the population regression line.
- To learn how to test hypotheses regarding
.
The parameter 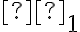 , the slope of the population regression line, is of primary importance in regression analysis because it gives the true rate of change in the mean
, the slope of the population regression line, is of primary importance in regression analysis because it gives the true rate of change in the mean  in response to a unit increase in the predictor variable
in response to a unit increase in the predictor variable  . For every unit increase in
. For every unit increase in  the mean of the response variable y changes by
the mean of the response variable y changes by 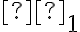 units, increasing if
units, increasing if 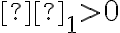 and decreasing if
and decreasing if 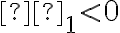 . We wish to construct confidence intervals for
. We wish to construct confidence intervals for 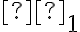 and test hypotheses about it.
and test hypotheses about it.
Confidence Intervals for 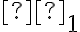
The slope  of the least squares regression line is a point estimate of
of the least squares regression line is a point estimate of 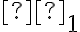 . A confidence interval for
. A confidence interval for 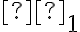 is given by the following formula.
is given by the following formula.
where
The assumptions listed in Section 10.3 "Modelling Linear Relationships with Randomness Present" must hold.
Definition
The statistic sε is called the sample standard deviation of errors. It estimates the standard deviation σ of the errors in the population of y-values for each fixed value of  (see Figure 10.5 "The Simple Linear Model Concept" in Section 10.3 "Modelling Linear Relationships with Randomness Present").
(see Figure 10.5 "The Simple Linear Model Concept" in Section 10.3 "Modelling Linear Relationships with Randomness Present").
Example 6
Construct the 95% confidence interval for the slope
Solution:
The point estimate
Confidence level 95% means 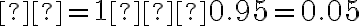 so
so 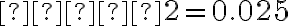 . From the row labeled
. From the row labeled  in Figure 12.3 "Critical Values of " we obtain
in Figure 12.3 "Critical Values of " we obtain  . Therefore
. Therefore
which gives the interval (0.1215,0.5661). We are 95% confident that the slope 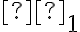 of the population regression line is between 0.1215 and 0.5661.
of the population regression line is between 0.1215 and 0.5661.
Example 7
Using the sample data in Table 10.3 "Data on Age and Value of Used Automobiles of a Specific Make and Model" construct a 90% confidence interval for the slopeSolution:
The point estimate
Confidence level 90% means
which gives the interval (−3.00,−1.10). We are 90% confident that the slope 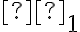 of the population regression line is between −3.00 and −1.10. In the context of the problem this means that for vehicles of this make and model between two and six years old we are 90% confident that for each additional year of age the average value of such a vehicle decreases by between $1,100 and $3,000.
of the population regression line is between −3.00 and −1.10. In the context of the problem this means that for vehicles of this make and model between two and six years old we are 90% confident that for each additional year of age the average value of such a vehicle decreases by between $1,100 and $3,000.
Testing Hypotheses About 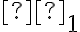
Hypotheses regarding 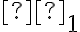 can be tested using the same five-step procedures, either the critical value approach or the p-value approach, that were introduced in Section 8.1 "The Elements of Hypothesis Testing" and Section 8.3 "The Observed Significance of a Test" of Chapter 8 "Testing Hypotheses". The null hypothesis always has the form
can be tested using the same five-step procedures, either the critical value approach or the p-value approach, that were introduced in Section 8.1 "The Elements of Hypothesis Testing" and Section 8.3 "The Observed Significance of a Test" of Chapter 8 "Testing Hypotheses". The null hypothesis always has the form 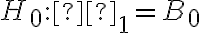 where
where  is a number determined from the statement of the problem. The three forms of the alternative hypothesis, with the terminology for each case, are:
is a number determined from the statement of the problem. The three forms of the alternative hypothesis, with the terminology for each case, are:
The value zero for  is of particular importance since in that case the null hypothesis is
is of particular importance since in that case the null hypothesis is 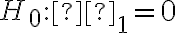 , which corresponds to the situation in which x is not useful for predicting y. For if
, which corresponds to the situation in which x is not useful for predicting y. For if  then the population regression line is horizontal, so the mean
then the population regression line is horizontal, so the mean  is the same for every value of
is the same for every value of  and we are just as well off in ignoring
and we are just as well off in ignoring  completely and approximating
completely and approximating  by its average value. Given two variables
by its average value. Given two variables  and
and  , the burden of proof is that
, the burden of proof is that  is useful for predicting
is useful for predicting  , not that it is not. Thus the phrase "test whether
, not that it is not. Thus the phrase "test whether  is useful for prediction of
is useful for prediction of  ," or words to that effect, means to perform the test
," or words to that effect, means to perform the test
The test statistic has Student's t-distribution with
The assumptions listed in Section 10.3 "Modelling Linear Relationships with Randomness Present" must hold.
Example 8
Test, at the 2% level of significance, whether the variable x is useful for predicting y based on the information in the five-point data set
Solution:
We will perform the test using the critical value approach.
- Step 1. Since
is useful for prediction of
precisely when the slope
of the population regression line is nonzero, the relevant test is
vs.@
- Step 2. The test statistic is
and has Student's t-distribution with
- Step 3. From Note 10.18 "Example 2",
and
. From Note 10.30 "Example 6",
. The value of the test statistic is therefore
- Step 4. Since the symbol in
is "≠" this is a two-tailed test, so there are two critical values
. Reading from the line in Figure 12.3 "Critical Values of " labeled
,
. The rejection region is
.
- Step 5. As shown in Figure 10.9 "Rejection Region and Test Statistic for " the test statistic falls in the rejection region. The decision is to reject
. In the context of the problem our conclusion is:
The data provide sufficient evidence, at the 2% level of significance, to conclude that the slope of the population regression line is nonzero, so thatis useful as a predictor of
.
Figure 10.9 Rejection Region and Test Statistic for Note 10.33 "Example 8"

Example 9
A car salesman claims that automobiles between two and six years old of the make and model discussed in Note 10.19 "Example 3" in Section 10.4 "The Least Squares Regression Line" lose more than $1,100 in value each year. Test this claim at the 5% level of significance.
Solution:
We will perform the test using the critical value approach.
- Step 1. In terms of the variables
and
, the salesman's claim is that if
is increased by 1 unit (one additional year in age), then y decreases by more than 1.1 units (more than $1,100). Thus his assertion is that the slope of the population regression line is negative, and that it is more negative than −1.1. In symbols,
. Since it contains an inequality, this has to be the alternative hypotheses. The null hypothesis has to be an equality and have the same number on the right hand side, so the relevant test is
vs.@
- Step 2. The test statistic is
and has Student's t-distribution with 8 degrees of freedom.
- Step 3. From Note 10.19 "Example 3",
and
. From Note 10.31 "Example 7",
. The value of the test statistic is therefore
- Step 4. Since the symbol in
is "<" this is a left-tailed test, so there is a single critical value
. Reading from the line in Figure 12.3 "Critical Values of " labeled
,
. The rejection region is (−∞,−1.860].
- Step 5. As shown in Figure 10.10 "Rejection Region and Test Statistic for " the test statistic falls in the rejection region. The decision is to reject
. In the context of the problem our conclusion is:
The data provide sufficient evidence, at the 5% level of significance, to conclude that vehicles of this make and model and in this age range lose more than $1,100 per year in value, on average.
Figure 10.10 Rejection Region and Test Statistic for Note 10.34 "Example 9"

 This text was adapted by Saylor Academy under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 License without attribution as requested by the work's original creator or licensor.
This text was adapted by Saylor Academy under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 License without attribution as requested by the work's original creator or licensor.