Using Factoring to Solve Quadratic Equations

Read these two articles, which give examples of how factoring is used to solve quadratic equations. Try to identify the factoring methods being used and why each step is performed. After you have reviewed the materials, complete a few practice problems and check your answers.

To solve a quadratic equation by factoring:

Put it in standard form: $ax2+bx+c=0$
Factor the left-hand side
Use the Zero Factor Law

Solve: $x^{2}=2-x$

Solution: Write a nice, clean list of equivalent equations.

$x^{2}=2-x$	Original equation
$x^{2}+x-2=0$	Put in standard form: subtract $2$ from both sides; add $x$ to both sides
$(x+2)(x-1)=0$	Factor the left-hand side
$x+2=0$ or $x-1=0$	Use the Zero Factor Law
$x=-2$ or $x=1$	Solve the simpler equations

Check by substituting into the original equation:

$(-2)^{2}=2-(-2)$ ; $4=4$ ; Check!

$(1)^{2}=2-1$ ; $1=1$ Check!

Solve: $(x+3)(x-2)=0$

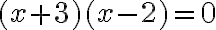
Solution: Do not multiply it out! If it is already in factored form, with zero on one side, then be happy that a lot of the work has already been done for you.

$(x+3)(x-2)=0$	Original equation
$x+3=0$ or $x-2=0$	Use the Zero Factor Law
$x=-3$ or $x=2$	Solve the simpler equations

Check by substituting into the original equation:

$(-3+3)(-3-2)=0$ ; $0=0$ Check!

$(2+3)(2-2)=0$ ; $0=0$ Check!

Solve: $(2x-3)(1-3x)=0$

Solution: Again, do not multiply it out! When you have a product on one side, and zero on the other side, then you are all set to use the Zero Factor Law.

$(2x-3)(1-3x)=0$	Original equation
$2x-3=0$ or $1-3x=0$	Use the Zero Factor Law
$2x=3$ or $1-3x$	Solve simpler equations
$x=\frac{3}{2}$ or $x=\frac{1}{3}$	Solve simpler equations

Check by substituting into the original equation:

$(2\cdot \frac{3}{2}-3)(1-3\cdot \frac{3}{2})=0$ ; $0=0$ Check!

$(2\cdot \frac{1}{3}+3)(1-3\cdot \frac{1}{3})=0$ ; $0=0$ Check!

Solve: $x^{2}+4x-5=0$

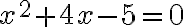
Solution: Note that it is already in standard form.

$x^{2}+4x-5=0$	Original equation
$(x+5)(x-1)=0$	Factor the left-hand side
$x+5=0$ or $x-1=0$	Use the Zero Factor Law
$x=-5$ or $x=1$	Solve the simpler equations

Check by substituting into the original equation:

$(-5)^{2}+4(-5)-5=0$ ; $25-20-5=0$ ; $0=0$ Check!

$1^{2}+4(1)-5+0$ ; $1+4-5=0$ ; $0=0$ Check!

Solve: $14=-5x+x^{2}$

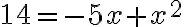
Solution:

$14=-5x+x^{2}$	Original equation
$x^{2}-5x-14=0$	Put in standard form: subtract $14$ from both sides; write in the conventional way
$(x-7)(x+2)=0$	Factor the left-hand side
$x-7=0$ or $x+2=0$	Use the Zero Factor Law
$x=7$ or $x=-2$	Solve the simpler equations

Check by substituting into the original equation:

$14=-5(7)+7^{2}$ ; $14=-35+49$ ; $14=14$ Check!

$14=-5(-2)+(-2)^{2}$ ; $14=10+4$ ; $14=14$ Check!

Solve: $6x=2x^{2}$

Solution: When there is no constant term, the factoring is much easier.

$6x=2x^{2}$	Original equation
$2x^{2}-6x=0$	Put in standard form: subtract $6x$ from both sides; write in the conventional way
$x^{2}-3x=0$	Optional step: divide both sides by $2$
$x(x-3)=0$	Factor the left-hand side
$x=0$ or $x-3=0$	Use the Zero Factor Law
$x=0$ or $x=3$	Solve the simpler equations