When investing in bonds, understanding their yield is of utmost importance. They reflect the length and interest to be paid to the investor. Here you will learn why yields are indicative of investors' expectations. How would you estimate interest rates in the future using the yield curve?
Using the Yield Curve to Estimate Interest Rates in the Future
Heath-Jarrow-Morton Framework
When it comes to predicting future interest rates, the Heath-Jarrow-Morton framework is considered a standard approach. It focuses on modeling the evolution of the interest rate curve (instantaneous forward rate curve in particular). The equation itself is a rather evolved derivation, incorporating bond prices, forward rates, risk free rates, the Wiener process, Leibniz's rule, and Fubini's Theorem. While the details of this calculation are a bit outside the scope of discussion here, the equation can ultimately be described as:
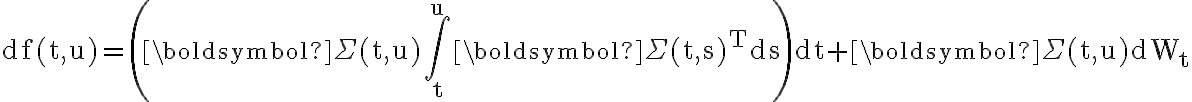
For the sake of this discussion, it suffices to say that the input of existing yield curves is useful in projected future interest rates under a number of varying perspectives.